Analiză detaliată a circuitului seriei RC
2024-05-08
20597
Circuitul seriei RC, format dintr -un rezistor și un condensator, servește ca o componentă fundamentală atât în proiectele de sistem electronic de bază, cât și avansate.Ajută la înțelegerea principiilor cheie, cum ar fi răspunsul la frecvență, schimbarea fazelor și filtrarea semnalului, care joacă un rol semnificativ în proiectarea circuitului și în procesarea semnalului.Această explorare acoperă elementele de bază teoretice și se extinde la aplicații practice prin experimente și simulări.Prin asamblarea fizică a circuitului sau modelarea acestuia digital, elevii pot înțelege vizual procesul de încărcare și efectele ionilor componente V ariat, ceea ce face ca conceptele complexe să fie mai accesibile și mai memorabile.
Catalog

Figura 1: Tensiuni de ieșire diferite ale circuitelor RC
Introducere în RC Circuit
Un circuit RC, scurt pentru circuitul de rezistență-capacitate, este fundamental în electronice pentru manipularea semnalelor prin rezistențe și condensatoare.Aceste circuite sunt cunoscute în special pentru capacitatea lor de a schimba fazele și semnalele de filtrare, folosind aranjamente simple ale acestor componente.Un circuit RC de bază, denumit adesea un circuit RC de prim ordin, include de obicei doar un rezistor și un condensator.
Într -o configurație tipică, tensiunea de intrare este aplicată la aranjarea seriei unui rezistor și a unui condensator.Ieșirea poate fi trasă fie de -a lungul rezistenței, fie a condensatorului, fiecare dând răspunsuri diferite la frecvențele semnalului datorită caracteristicilor unice ale condensatorului.Această versatilitate permite circuitelor RC să îndeplinească o varietate de roluri în dispozitivele electronice, cum ar fi semnalele de cuplare și filtrare sau chiar transformarea formelor de undă atunci când sunt supuse unei tensiuni de pas.
Circuitul RC poate fi configurat în mai multe moduri-serii, paralel sau o combinație a ambelor, cunoscute sub numele de seria-paralelă.Fiecare configurație afectează diferit frecvențele semnalului: conexiunile în serie tind să atenueze frecvențele joase, în timp ce conexiunile paralele sunt utilizate pentru a amortiza frecvențe mai mari.Această diferență se datorează în primul rând modului în care rezistențele și condensatoarele interacționează cu circuitul;Rezistențele se opun direct curentului în timp ce condensatorii îl stochează și îl eliberează, impactând modul în care circuitul răspunde la diferite frecvențe.
Spre deosebire de circuitele care includ inductori, cum ar fi circuitele LC, circuitele RC simple nu pot rezona, deoarece rezistențele nu stochează energie.Acest atribut influențează în mod distinct modul în care sunt utilizate circuitele RC, concentrându -se pe capacitatea lor de filtrare, mai degrabă decât de stocare de energie sau de rezonanță.Fiecare configurație servește un scop specific, făcând circuitele RC instrumente versatile atât în studiul teoretic, cât și în aplicarea practică în proiectarea electronică.
Circuitul seriei RC
Un circuit din seria RC, compus în esență dintr -un rezistor (R) și un condensator (C.) În serie, funcționează pe un principiu simplu.Când întrerupătorul circuitului este închis, condensatorul începe să se încarce din tensiunea aplicată (V), inițierea unui flux de curent prin circuit.Pe măsură ce condensatorul se încarcă, curentul crește treptat până când condensatorul își atinge capacitatea, moment în care încetează să accepte taxa, iar curentul se stabilizează la valoarea sa maximă, calculată ca 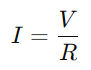 .
.
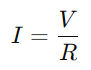 .
.Procesul de încărcare al condensatorului poate fi descris matematic de ecuație 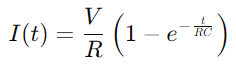 , unde sunt curentul, V este tensiunea, R este rezistența, C. este capacitatea, t este timpul și e este baza logaritmului natural.Această formulă reflectă modul în care curentul se schimbă în timp pe măsură ce condensatorul se încarcă, cu produsul valorilor de rezistență și capacitate (RC) care definește constanta de timp a circuitului, indicând viteza cu care condensatorul încărcă.
, unde sunt curentul, V este tensiunea, R este rezistența, C. este capacitatea, t este timpul și e este baza logaritmului natural.Această formulă reflectă modul în care curentul se schimbă în timp pe măsură ce condensatorul se încarcă, cu produsul valorilor de rezistență și capacitate (RC) care definește constanta de timp a circuitului, indicând viteza cu care condensatorul încărcă.
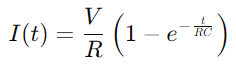 , unde sunt curentul, V este tensiunea, R este rezistența, C. este capacitatea, t este timpul și e este baza logaritmului natural.Această formulă reflectă modul în care curentul se schimbă în timp pe măsură ce condensatorul se încarcă, cu produsul valorilor de rezistență și capacitate (RC) care definește constanta de timp a circuitului, indicând viteza cu care condensatorul încărcă.
, unde sunt curentul, V este tensiunea, R este rezistența, C. este capacitatea, t este timpul și e este baza logaritmului natural.Această formulă reflectă modul în care curentul se schimbă în timp pe măsură ce condensatorul se încarcă, cu produsul valorilor de rezistență și capacitate (RC) care definește constanta de timp a circuitului, indicând viteza cu care condensatorul încărcă.
Figura 2: Circuitul seriei RC
Descărcarea are loc atunci când comutatorul este deschis, inversând procesul: energia stocată în condensator este eliberată, determinând curgerea curentului în direcția opusă până când condensatorul este scurs.Acest ciclu de încărcare și descărcare este crucial în aplicații precum conversia semnalului, filtrarea și circuitele de sincronizare datorită modului previzibil în care se schimbă curentul și tensiunea.

Figura 3: Seria RC Short Circuit
Comportamentul circuitului seriei RC variază, de asemenea, în funcție de frecvență.La frecvențe joase, condensatorul acționează mai mult ca un circuit deschis, împiedicând foarte mult fluxul de curent.Pe măsură ce frecvența crește, reactanța capacitivă scade, făcând mai ușor să treacă curentul.Această modificare a impedanței cu frecvența permite circuitului seriei RC să acționeze ca un filtru, atenuând selectiv frecvențele sub un anumit prag (frecvența de rotire 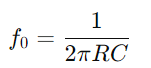 )
)
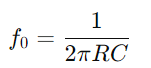 )
)
Figura 4: Încărcarea și descărcarea circuitelor din seria RC
În plus față de operațiunile în stare de echilibru, circuitele RC sunt studiate și pentru răspunsurile lor tranzitorii atunci când sunt supuse modificărilor bruște ale tensiunii, cum ar fi atunci când o sursă de alimentare cu curent continuu este pornită sau oprită.Acest scenariu este denumit un proces tranzitoriu, în care circuitul trece de la o stare stabilă la alta.Dinamica acestui proces depinde semnificativ de constanta de timp RC, care guvernează cât de repede reacționează circuitul la modificări.
În cele din urmă, circuitele din seria RC servesc mai multe funcții atât în aplicațiile DC cât și în curent alternativ, gestionând sarcini, de la întârzierea semnalelor până la integrarea sau cuplarea diferitelor elemente de circuit.Această versatilitate provine din interacțiunile unice dintre rezistență și condensator, care determină împreună răspunsul general al circuitului la modificările tensiunii și frecvenței.

Figura 5: Diagrama circuitului din seria RC și formula de frecvență
Într -un circuit din seria RC, interacțiunea dintre rezistență (R) și condensatorul (C) influențează atât debitul curent, cât și distribuția tensiunii.Rolul principal al rezistenței este de a regla fluxul curent.Această relație este cuantificată prin legea lui Ohm, care afirmă 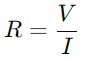 , unde V este tensiune și I este curent.În esență, rezistența acționează ca un blocaj, controlând cât de multă energie electrică poate trece la un moment dat.
, unde V este tensiune și I este curent.În esență, rezistența acționează ca un blocaj, controlând cât de multă energie electrică poate trece la un moment dat.
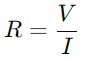 , unde V este tensiune și I este curent.În esență, rezistența acționează ca un blocaj, controlând cât de multă energie electrică poate trece la un moment dat.
, unde V este tensiune și I este curent.În esență, rezistența acționează ca un blocaj, controlând cât de multă energie electrică poate trece la un moment dat.Funcția condensatorului este puțin mai complexă, deoarece stochează temporar energia electrică și apoi o eliberează înapoi în circuit.Tensiunea de pe condensator (VC) se corelează cu taxa stocată (Î) și este calculat folosind formula 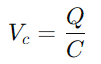 .Această relație evidențiază capacitatea condensatorului de a menține încărcarea, impactând direct tensiunea pe care o prezintă.În timpul funcționării, dinamica încărcării și descărcării condensatorului este vitală pentru înțelegerea circuitelor RC.Constanta de timp (τ), definit ca
.Această relație evidențiază capacitatea condensatorului de a menține încărcarea, impactând direct tensiunea pe care o prezintă.În timpul funcționării, dinamica încărcării și descărcării condensatorului este vitală pentru înțelegerea circuitelor RC.Constanta de timp (τ), definit ca  , măsoară cât de repede condensatorul ajunge la aproximativ 63,2% din tensiunea completă furnizată de sursă (V0)Această constantă de acest timp indică modul în care circuitul se adaptează la modificările de intrare, proprietățile rezistenței și condensatorului dictând ritmul acestor ajustări.
, măsoară cât de repede condensatorul ajunge la aproximativ 63,2% din tensiunea completă furnizată de sursă (V0)Această constantă de acest timp indică modul în care circuitul se adaptează la modificările de intrare, proprietățile rezistenței și condensatorului dictând ritmul acestor ajustări.
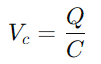 .Această relație evidențiază capacitatea condensatorului de a menține încărcarea, impactând direct tensiunea pe care o prezintă.În timpul funcționării, dinamica încărcării și descărcării condensatorului este vitală pentru înțelegerea circuitelor RC.Constanta de timp (τ), definit ca
.Această relație evidențiază capacitatea condensatorului de a menține încărcarea, impactând direct tensiunea pe care o prezintă.În timpul funcționării, dinamica încărcării și descărcării condensatorului este vitală pentru înțelegerea circuitelor RC.Constanta de timp (τ), definit ca  , măsoară cât de repede condensatorul ajunge la aproximativ 63,2% din tensiunea completă furnizată de sursă (V0)Această constantă de acest timp indică modul în care circuitul se adaptează la modificările de intrare, proprietățile rezistenței și condensatorului dictând ritmul acestor ajustări.
, măsoară cât de repede condensatorul ajunge la aproximativ 63,2% din tensiunea completă furnizată de sursă (V0)Această constantă de acest timp indică modul în care circuitul se adaptează la modificările de intrare, proprietățile rezistenței și condensatorului dictând ritmul acestor ajustări.Tensiunea de pe condensator în orice moment în timpul acuzației este dată de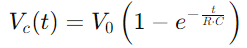 , ilustrând o creștere neliniară pe măsură ce condensatorul se umple.Această ecuație descrie modul în care rata de încărcare încetinește pe măsură ce condensatorul se apropie de capacitate maximă.
, ilustrând o creștere neliniară pe măsură ce condensatorul se umple.Această ecuație descrie modul în care rata de încărcare încetinește pe măsură ce condensatorul se apropie de capacitate maximă.
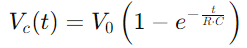 , ilustrând o creștere neliniară pe măsură ce condensatorul se umple.Această ecuație descrie modul în care rata de încărcare încetinește pe măsură ce condensatorul se apropie de capacitate maximă.
, ilustrând o creștere neliniară pe măsură ce condensatorul se umple.Această ecuație descrie modul în care rata de încărcare încetinește pe măsură ce condensatorul se apropie de capacitate maximă.În schimb, în timpul externării, tensiunea condensatorului scade în funcție de 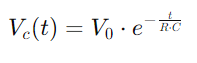 , portretizând o scădere liniară a energiei stocate în timp.Acest proces oferă o imagine clară a modului în care energia este eliberată din condensator înapoi în circuit.În aplicațiile de curent alternativ, diferența de fază dintre tensiune și curent, φ, devine critic.Această diferență, calculată ca
, portretizând o scădere liniară a energiei stocate în timp.Acest proces oferă o imagine clară a modului în care energia este eliberată din condensator înapoi în circuit.În aplicațiile de curent alternativ, diferența de fază dintre tensiune și curent, φ, devine critic.Această diferență, calculată ca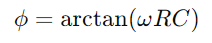 unde ω reprezintă frecvența unghiulară, arată întârzierea cauzată de condensator, care afectează momentul dintre momentul în care curge curentul și modificările de tensiune între componente.
unde ω reprezintă frecvența unghiulară, arată întârzierea cauzată de condensator, care afectează momentul dintre momentul în care curge curentul și modificările de tensiune între componente.
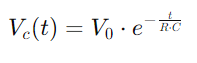 , portretizând o scădere liniară a energiei stocate în timp.Acest proces oferă o imagine clară a modului în care energia este eliberată din condensator înapoi în circuit.În aplicațiile de curent alternativ, diferența de fază dintre tensiune și curent, φ, devine critic.Această diferență, calculată ca
, portretizând o scădere liniară a energiei stocate în timp.Acest proces oferă o imagine clară a modului în care energia este eliberată din condensator înapoi în circuit.În aplicațiile de curent alternativ, diferența de fază dintre tensiune și curent, φ, devine critic.Această diferență, calculată ca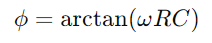 unde ω reprezintă frecvența unghiulară, arată întârzierea cauzată de condensator, care afectează momentul dintre momentul în care curge curentul și modificările de tensiune între componente.
unde ω reprezintă frecvența unghiulară, arată întârzierea cauzată de condensator, care afectează momentul dintre momentul în care curge curentul și modificările de tensiune între componente.În general, rezistența limitează și direcționează fluxul de curent în timp ce condensatorul depozitează și modulează tensiunea.Împreună, ei determină caracteristicile de răspuns ale circuitului, cum ar fi cât de repede se poate încărca și descărca și schimbările de fază care apar în scenarii de curent alternativ.Acest comportament combinat stă la baza operațiunilor fundamentale ale circuitelor din seria RC, ceea ce le face integrale în diferite aplicații electronice.
Ecuații de bază ale circuitului seriei RC
Pentru a înțelege comportamentul unui circuit din seria RC, este crucial să începeți cu ecuațiile de bază care descriu răspunsul său la modificările tensiunii de intrare.Presupunem că avem o tensiune de intrare în schimbare reprezentată ca Vin (t), cu tensiunea de -a lungul rezistenței etichetate ca VR (T) și peste condensator ca VC (T).Într -un circuit de serie, același curent, I (T) Se curge atât prin rezistență, cât și prin condensator.
Aplicarea legii tensiunii (KVL) a lui Kirchhoff, care afirmă că tensiunea totală în jurul oricărei bucle închise într -un circuit trebuie să fie egală cu zero, descoperim că tensiunea de intrare este egală cu suma tensiunilor de -a lungul rezistenței și a condensatorului:

Tensiunea de -a lungul rezistenței poate fi calculată folosind Legea lui Ohm:
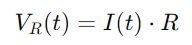
Pentru condensator, tensiunea VC (t) este legată de sarcina Q (t) pe care o deține, dată de:
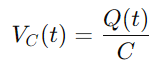
Deoarece curentul este definit ca rata de flux de încărcare, avem:
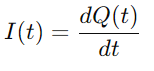
Prin înlocuire Q (T) în ecuație pentru VC (T), și folosind derivatul încărcăturii I (T), derivăm ecuația diferențială de bază pentru circuitul seriei RC:

Înlocuirea în continuare Q (T) cu integral din I (T), obținem:
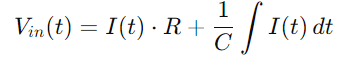
Pentru curentul I (t), având în vedere rata de modificare a tensiunii pe condensator, folosim:
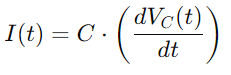
Integrarea tuturor acestor relații ne oferă ecuația diferențială care descrie tensiunea de pe condensator:
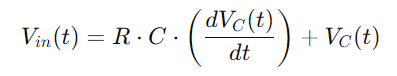
Aceasta este o ecuație diferențială liniară de prim ordin care surprinde schimbarea de tensiune dependentă de timp în întregime.Rezolvarea acestei ecuații ne permite să descriem cu exactitate modul în care evoluează tensiunea condensatorului.Această înțelegere este fundamentală pentru analizarea atât a ciclurilor de încărcare, cât și pentru descărcarea condensatorului, precum și răspunsul circuitului la diferite frecvențe.Această abordare cuprinzătoare oferă o perspectivă profundă asupra caracteristicilor dinamice ale circuitului seriei RC.

Figura 6: Ecuația diferențială de tensiune
Impedanța circuitului seriei RC
Pentru a rescrie descrierea unui circuit din seria RC, cu accent pe interacțiunea umană și o explicație directă, simplificată, să îmbunătățim experiențele tangibile și operațiunile pas cu pas implicate, menținând în același timp mesajul și coerența de bază:
Într -un circuit din seria RC, rezistența și condensatorul lucrează în tandem pentru a controla fluxul de electricitate, crucial atunci când se ocupă cu curenții alternativi.Impedanța totală a circuitului, reprezentată ca 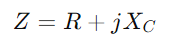 , combină rezistența R și Reactanța capacitivă XC.Caracteristica cheie a acestei configurații este că valorile impedanței pentru ambele componente variază în funcție de modificările de frecvență.Pe măsură ce frecvența crește, impedanța condensatorului scade, permițând trecerea mai mult curent, în timp ce rezistența rămâne în esență constantă.
, combină rezistența R și Reactanța capacitivă XC.Caracteristica cheie a acestei configurații este că valorile impedanței pentru ambele componente variază în funcție de modificările de frecvență.Pe măsură ce frecvența crește, impedanța condensatorului scade, permițând trecerea mai mult curent, în timp ce rezistența rămâne în esență constantă.
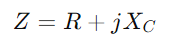 , combină rezistența R și Reactanța capacitivă XC.Caracteristica cheie a acestei configurații este că valorile impedanței pentru ambele componente variază în funcție de modificările de frecvență.Pe măsură ce frecvența crește, impedanța condensatorului scade, permițând trecerea mai mult curent, în timp ce rezistența rămâne în esență constantă.
, combină rezistența R și Reactanța capacitivă XC.Caracteristica cheie a acestei configurații este că valorile impedanței pentru ambele componente variază în funcție de modificările de frecvență.Pe măsură ce frecvența crește, impedanța condensatorului scade, permițând trecerea mai mult curent, în timp ce rezistența rămâne în esență constantă.Impedanța, notată ca Z. și măsurat în ohmi (ω), joacă un rol critic în determinarea modului în care circuitul reacționează la curent alternativ.Ca în circuitele din seria RL, rezistența R și reactanță capacitivă xC. a unui circuit RC formează un triunghi cunoscut sub numele de Triunghiul impedanței.Acest triunghi se raportează îndeaproape cu triunghiul de tensiune și, prin aplicarea teoremei pitagoreene, puteți calcula impedanța totală a circuitului.

Figura 7: Formula de calcul a circuitului din seria RC
Când vine vorba de aplicații practice, luați în considerare căștile, care folosesc aceste principii.Căștile cu impedanță ridicată, care depășesc adesea 200 de ohmi, sunt de obicei utilizate cu computere desktop, amplificatoare de putere și echipamente audio profesionale.Aceste modele de mare impedanță se potrivesc bine cu capacitățile de ieșire ale electronicelor de calitate profesională.Când utilizați aceste căști, este crucial să reglați treptat volumul pentru a evita supraîncărcarea și deteriorarea componentelor interne delicate, cum ar fi bobina vocală.
În schimb, căștile cu impedanță scăzută, de obicei sub 50 de ohmi, sunt preferate pentru dispozitive portabile precum CD players, playere MD sau MP3.Aceste căști necesită mai puțină putere pentru a oferi audio de înaltă calitate, ceea ce le face ideale pentru utilizare mobilă.Cu toate acestea, acestea necesită, de asemenea, o atenție atentă asupra nivelurilor de sensibilitate pentru a asigura performanța optimă și pentru a preveni deteriorarea căștilor sau auzului.

Figura 8: Diagrama de impedanță a circuitului seriei RC
Proceduri de admitere și analiză ale circuitelor din seria RC
Admiterea măsoară cât de ușor poate efectua un circuit din seria RC, calculat ca invers al impedanței (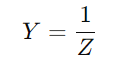 )Această valoare integrează atât rezistența (R) și reactanța (X) a circuitului.Rezistența se opune fluxului de curent prin transformarea energiei electrice în căldură, în timp ce reactanța stochează temporar energia în circuit.
)Această valoare integrează atât rezistența (R) și reactanța (X) a circuitului.Rezistența se opune fluxului de curent prin transformarea energiei electrice în căldură, în timp ce reactanța stochează temporar energia în circuit.
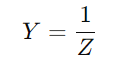 )Această valoare integrează atât rezistența (R) și reactanța (X) a circuitului.Rezistența se opune fluxului de curent prin transformarea energiei electrice în căldură, în timp ce reactanța stochează temporar energia în circuit.
)Această valoare integrează atât rezistența (R) și reactanța (X) a circuitului.Rezistența se opune fluxului de curent prin transformarea energiei electrice în căldură, în timp ce reactanța stochează temporar energia în circuit.Pentru a calcula admiterea
Începeți prin a scrie impedanța 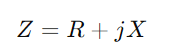 , unde R înseamnă rezistență, X pentru reactanță și J. este unitatea imaginară.Folosiți formula y = 1/(R + JX)Această operație implică numere complexe și ne oferă
, unde R înseamnă rezistență, X pentru reactanță și J. este unitatea imaginară.Folosiți formula y = 1/(R + JX)Această operație implică numere complexe și ne oferă 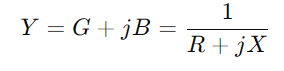 .Aici, G este conductanța (capacitatea reală a fluxului de curent) și B este suscepția (capacitatea circuitului de a reacționa la modificările curentului).
.Aici, G este conductanța (capacitatea reală a fluxului de curent) și B este suscepția (capacitatea circuitului de a reacționa la modificările curentului).
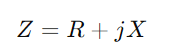 , unde R înseamnă rezistență, X pentru reactanță și J. este unitatea imaginară.Folosiți formula y = 1/(R + JX)Această operație implică numere complexe și ne oferă
, unde R înseamnă rezistență, X pentru reactanță și J. este unitatea imaginară.Folosiți formula y = 1/(R + JX)Această operație implică numere complexe și ne oferă 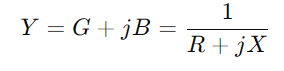 .Aici, G este conductanța (capacitatea reală a fluxului de curent) și B este suscepția (capacitatea circuitului de a reacționa la modificările curentului).
.Aici, G este conductanța (capacitatea reală a fluxului de curent) și B este suscepția (capacitatea circuitului de a reacționa la modificările curentului).
Figura 9: Calculator de impedanță a circuitului RC din seria RC
Acest calcul relevă nu doar conductivitatea circuitului, ci și caracteristicile sale dinamice de răspuns, cruciale pentru analiza circuitului AC.Conductanța și suscepția, luate împreună, indică modul în care circuitul trece curent și cum stochează și eliberează energie.

Figura 10: Formula unghiului de fază
Aplicație practică
Inginerii folosesc valori de admitere pentru a îmbunătăți proiectarea circuitului, în special în aplicații de înaltă frecvență, cum ar fi circuitele de frecvență radio.Reglarea admiterii ajută la potrivirea impedanței, la reducerea reflecției semnalului și la creșterea eficienței transmisiei.
Studierea răspunsului la admitere, inginerii pot evalua și prezice performanța circuitului în diferite condiții, cum ar fi răspunsul la frecvență, stabilitatea și sensibilitatea.Echipați cu un osciloscop și un generator de semnal pentru a măsura tensiunea și curentul circuitului la diferite frecvențe.Concentrați -vă în special pe frecvența de întrerupere pentru a testa predicțiile teoretice și pentru a le valida împotriva observațiilor practice.Pentru circuite AC, începeți prin determinarea reactanței (XC) a condensatorului cu 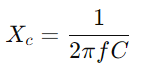 , unde f este frecvența semnalului.Calculați impedanța totală
, unde f este frecvența semnalului.Calculați impedanța totală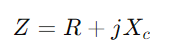 Și apoi admiterea
Și apoi admiterea 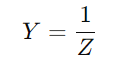 .
.
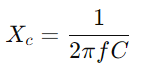 , unde f este frecvența semnalului.Calculați impedanța totală
, unde f este frecvența semnalului.Calculați impedanța totală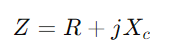 Și apoi admiterea
Și apoi admiterea 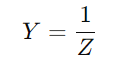 .
.Analizați diferența de fază folosind 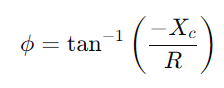 Pentru a înțelege modificarea formei semnalului.Examinați modul în care circuitul gestionează diferite frecvențe, remarcând în special comportamentul la frecvența de întrerupere
Pentru a înțelege modificarea formei semnalului.Examinați modul în care circuitul gestionează diferite frecvențe, remarcând în special comportamentul la frecvența de întrerupere 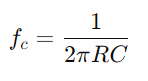 , unde circuitul trece de la trecerea la semnale bloc.Evaluarea modului în care impedanța și diferența de fază variază cu frecvența, este crucială pentru proiectarea filtrelor eficiente și a procesoarelor de semnal.Discutați cum selectivitatea frecvenței, schimbările de fază și atenuarea semnalului datorită proprietăților circuitului afectează aplicații practice precum filtrarea și reglarea electronică.
, unde circuitul trece de la trecerea la semnale bloc.Evaluarea modului în care impedanța și diferența de fază variază cu frecvența, este crucială pentru proiectarea filtrelor eficiente și a procesoarelor de semnal.Discutați cum selectivitatea frecvenței, schimbările de fază și atenuarea semnalului datorită proprietăților circuitului afectează aplicații practice precum filtrarea și reglarea electronică.
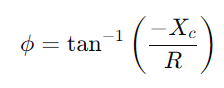 Pentru a înțelege modificarea formei semnalului.Examinați modul în care circuitul gestionează diferite frecvențe, remarcând în special comportamentul la frecvența de întrerupere
Pentru a înțelege modificarea formei semnalului.Examinați modul în care circuitul gestionează diferite frecvențe, remarcând în special comportamentul la frecvența de întrerupere 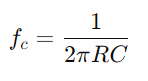 , unde circuitul trece de la trecerea la semnale bloc.Evaluarea modului în care impedanța și diferența de fază variază cu frecvența, este crucială pentru proiectarea filtrelor eficiente și a procesoarelor de semnal.Discutați cum selectivitatea frecvenței, schimbările de fază și atenuarea semnalului datorită proprietăților circuitului afectează aplicații practice precum filtrarea și reglarea electronică.
, unde circuitul trece de la trecerea la semnale bloc.Evaluarea modului în care impedanța și diferența de fază variază cu frecvența, este crucială pentru proiectarea filtrelor eficiente și a procesoarelor de semnal.Discutați cum selectivitatea frecvenței, schimbările de fază și atenuarea semnalului datorită proprietăților circuitului afectează aplicații practice precum filtrarea și reglarea electronică.Această abordare descompune procesele operaționale în pași gestionați, îmbogățind înțelegerea utilizatorului cu informații practice privind manipularea și analizarea circuitelor din seria RC.

Figura 11: Caracteristicile circuitelor din seria RC
Diagrama fazorică a circuitului seriei RC
Într -un circuit din seria RC, toate elementele împărtășesc același curent datorită configurației seriei lor.Acest curent uniform acționează ca o bază de bază pentru diagrama noastră fazor, care ajută la vizualizarea relației dintre diferite tensiuni și curenți din circuit.Să desemnăm acest curent I ca fazor de referință, poziționat la zero grade pe diagramă.În diagramă, curentul I este setat orizontal la dreapta, stabilind linia de referință de grad zero.Tensiunea de -a lungul rezistenței (UR) este în fază cu curentul, deoarece rezistențele nu provoacă nicio schimbare de fază.Astfel, UR este desenat ca un vector orizontal în aceeași direcție ca I, extinzându -se de la origine.

Figura 12: Diagrama fazorului din seria RC
În schimb, tensiunea de pe condensator (UC.) conduce curentul cu 90 de grade din cauza proprietății capacitive de întârziere a fazei curente.Această tensiune este reprezentată de un vector vertical îndreptat în sus, pornind de la vârful UR vector.Tensiunea totală U în circuit este suma vectorială a U Rand UC..Această sumă formează un triunghi drept cu UR şi UC. ca laturi adiacente și opuse, respectiv.Hipotenuza acestui triunghi, care se extinde de la origine la vârful UC. vector, reprezintă U.
Curentul sinusoidal prin circuit este dat de păcat (ωt), unde IM este amplitudinea maximă curentă și ω este frecvența unghiulară.În consecință, tensiunea de -a lungul rezistenței este 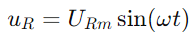 , oglindind forma de undă curentă.Tensiunea de pe condensator este dată de
, oglindind forma de undă curentă.Tensiunea de pe condensator este dată de 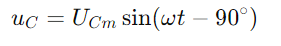 , indicând o deplasare de fază de -90 ° (sau 90 de grade înaintea curentului).Triunghiul drept al diagramei fazorului clarifică asta
, indicând o deplasare de fază de -90 ° (sau 90 de grade înaintea curentului).Triunghiul drept al diagramei fazorului clarifică asta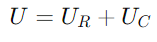 este nu numai în mărime, ci și în relația de fază, cu vectorul tensiunii terminale (U) completarea triunghiului.
este nu numai în mărime, ci și în relația de fază, cu vectorul tensiunii terminale (U) completarea triunghiului.
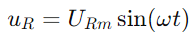 , oglindind forma de undă curentă.Tensiunea de pe condensator este dată de
, oglindind forma de undă curentă.Tensiunea de pe condensator este dată de 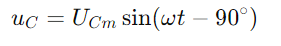 , indicând o deplasare de fază de -90 ° (sau 90 de grade înaintea curentului).Triunghiul drept al diagramei fazorului clarifică asta
, indicând o deplasare de fază de -90 ° (sau 90 de grade înaintea curentului).Triunghiul drept al diagramei fazorului clarifică asta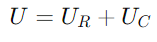 este nu numai în mărime, ci și în relația de fază, cu vectorul tensiunii terminale (U) completarea triunghiului.
este nu numai în mărime, ci și în relația de fază, cu vectorul tensiunii terminale (U) completarea triunghiului.
Figura 13: Diagrama fazorului de tensiune a circuitului seriei RC
Puncte cheie în analizarea circuitelor RC din seria
Impedanță în circuitul rc din seria RC, reprezentat ca Z., combină rezistența (R) și efectul reactiv al capacității într -o singură măsură care variază cu frecvența semnalului.Este exprimat matematic ca 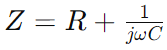 , unde ω este frecvența unghiulară și C. este capacitatea.Aici, R constituie partea reală a impedanței și
, unde ω este frecvența unghiulară și C. este capacitatea.Aici, R constituie partea reală a impedanței și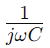 reprezintă partea imaginară, indicând modul în care condensatorul influențează circuitul.
reprezintă partea imaginară, indicând modul în care condensatorul influențează circuitul.
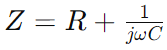 , unde ω este frecvența unghiulară și C. este capacitatea.Aici, R constituie partea reală a impedanței și
, unde ω este frecvența unghiulară și C. este capacitatea.Aici, R constituie partea reală a impedanței și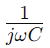 reprezintă partea imaginară, indicând modul în care condensatorul influențează circuitul.
reprezintă partea imaginară, indicând modul în care condensatorul influențează circuitul.Modul în care se modifică impedanța cu frecvența este pivot pentru utilizarea circuitelor RC din seria în aplicațiile de filtrare.La frecvențe inferioare, circuitul prezintă o impedanță mai mare, blocând eficient aceste frecvențe.În schimb, la frecvențe mai mari, impedanța scade, permițând aceste frecvențe să treacă mai liber.Acest comportament face ca circuitele RC din serie să fie ideale pentru sarcini precum filtrarea zgomotului nedorit de joasă frecvență sau trecerea semnalelor de înaltă frecvență.

Figura 14: Diagrama vectorială impedanță a circuitului seriei RC
Concluzie
De la filtrarea frecvențelor nedorite până la conturarea răspunsurilor semnalului, circuitul seriei RC este instrumental într -o gamă largă de funcții electronice.Înțelegerea principiilor de bază, cum ar fi impedanța, relațiile fazor și comportamentul dependent de frecvență al acestor circuite, inginerii și proiectanții sunt echipate pentru a face soluții de meșteșuguri care gestionează eficient integritatea semnalului în sistemele electronice complexe.Examinarea detaliată a acestor circuite, susținută de analiza matematică și reprezentări vizuale, cum ar fi diagramele fazor, oferă o perspectivă cuprinzătoare, care este importantă pentru oricine dorește să -și aprofundeze înțelegerea dinamicii circuitului electronic sau pentru a -și îmbunătăți abilitățile practice în proiectarea circuitului și rezolvarea problemelor.
Întrebări frecvente [FAQ]
1. Care este principiul circuitului RC?
Principiul unui circuit RC (rezistență-capacitor) se învârte în jurul proceselor de încărcare și descărcare a condensatorului prin rezistență.În acest circuit, capacitatea condensatorului de a stoca și elibera energia electrică interacționează cu rezistorul, care controlează viteza cu care condensatorul percepe sau descărcări.
2. De ce are un curent de plumb RC?
Într -un circuit RC, curentul conduce tensiunea pe condensator, deoarece condensatorul trebuie să înceapă încărcarea înainte de creșterea tensiunii sale.Deoarece curentul curge în condensator pentru a -l încărca, curentul atinge vârfurile înainte de tensiunea de pe condensator să atingă maximul său.Acest efect provoacă o schimbare de fază în care faza curentă conduce faza de tensiune cu până la 90 de grade, în funcție de frecvența semnalului de intrare.
3. Cum se schimbă tensiunea într -un circuit RC?
Schimbarea de tensiune într -un circuit RC în timpul încărcării este descrisă de o funcție exponențială.Când se aplică o tensiune, tensiunea de pe condensator crește inițial rapid, apoi încetinește pe măsură ce se apropie de tensiunea de alimentare.Matematic, acest lucru este exprimat ca 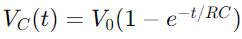 , unde VC.(T) este tensiunea de -a lungul condensatorului la momentul t, v0 este tensiunea de alimentare, iar RC este constanta de timp a circuitului, determinând cât de repede se încarcă condensatorul.În schimb, în timpul descărcării, tensiunea de pe condensator scade exponențial, după ecuație
, unde VC.(T) este tensiunea de -a lungul condensatorului la momentul t, v0 este tensiunea de alimentare, iar RC este constanta de timp a circuitului, determinând cât de repede se încarcă condensatorul.În schimb, în timpul descărcării, tensiunea de pe condensator scade exponențial, după ecuație 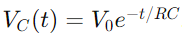 .
.
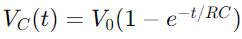 , unde VC.(T) este tensiunea de -a lungul condensatorului la momentul t, v0 este tensiunea de alimentare, iar RC este constanta de timp a circuitului, determinând cât de repede se încarcă condensatorul.În schimb, în timpul descărcării, tensiunea de pe condensator scade exponențial, după ecuație
, unde VC.(T) este tensiunea de -a lungul condensatorului la momentul t, v0 este tensiunea de alimentare, iar RC este constanta de timp a circuitului, determinând cât de repede se încarcă condensatorul.În schimb, în timpul descărcării, tensiunea de pe condensator scade exponențial, după ecuație 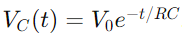 .
. DESPRE NOI
Satisfacția clienților de fiecare dată.Încredere reciprocă și interese comune.
DESPRE NOI
Satisfacția clienților de fiecare dată.Încredere reciprocă și interese comune.
test de functionare.Cele mai mari produse rentabile și cel mai bun serviciu este angajamentul nostru etern.
Articol fierbinte
- Sunt CR2032 și CR2016 interschimbabile
- MOSFET: definiție, principiu de lucru și selecție
- Instalarea și testarea releului, interpretarea diagramelor de cablare a releului
- CR2016 vs. CR2032 Care este diferența
- NPN vs. PNP: Care este diferența?
- ESP32 vs STM32: Care microcontroller este mai bun pentru tine?
- LM358 Amplificator operațional dual Ghid cuprinzător: Pinuts, diagrame de circuit, echivalente, exemple utile
- CR2032 vs DL2032 vs CR2025 Ghid de comparație
- Înțelegerea diferențelor ESP32 și ESP32-S3 Analiza tehnică și de performanță
- Analiză detaliată a circuitului seriei RC
 Analiza în profunzime a 1N4148 diode: moduri de operare, specificații și scenarii de utilizare
Analiza în profunzime a 1N4148 diode: moduri de operare, specificații și scenarii de utilizare
2024-05-08
 Înțelegerea tipurilor și utilizărilor pompelor de deplasare dinamice și pozitive
Înțelegerea tipurilor și utilizărilor pompelor de deplasare dinamice și pozitive
2024-05-07
Număr de piesă fierbinte
 CGA2B1X7R1A224M050BC
CGA2B1X7R1A224M050BC CL05C040BB5NNNC
CL05C040BB5NNNC CL02B121KP2NNNC
CL02B121KP2NNNC GRM033R71A682MA01J
GRM033R71A682MA01J GRM1555C1E2R4CA01D
GRM1555C1E2R4CA01D CC1206JKNPOCBN680
CC1206JKNPOCBN680 TMK316C106ML-T
TMK316C106ML-T TAP105K020CRW
TAP105K020CRW TAJY475M050RNJ
TAJY475M050RNJ ZXMP6A16KTC
ZXMP6A16KTC
- CY8C3446PVI-102
- LFE3-17EA-6MG328C
- AT90LS8535-4AC
- ACJ2112P
- MAX2640EUT+T
- VI-J31-EW
- VE-J13-IZ
- EPM7032BTI44-5
- 1MBI200HH-120L-50
- 2MBI300UC-120-50
- SKM195GAL062D
- VI-J3Y-EW/F1
- T491X227M010ZTZV16
- ADS5277IPFPT
- LT1461AIS8-3#TRPBF
- LTM8067IY#PBF
- DAC7731EB
- SN65LVDS302ZQER
- BD7902CFS-E2
- BTS3800SL
- IC1114-F48LQ
- K9F2G08U0C-BIB0
- MAX6193CESA
- PSMN030-60YS
- R7F7010243AFP#KA2
- S-8244AABFN-CEBT2S
- S29GL032N90TF104
- TPA6030A4PWR
- UPD705100GJ-100-8EU
- UPD78F0513DGB-UES-A
- ADP3193J
- HD74HC373RPEL
- UM62S256AV-70LL
- M04-0805GC
- XC3S250E-4PQS208C
- XBRIDGE1.0
- YGW60N65F1
- Si5517DU
- MOC3041IC